EP1K10TC100-3 Altera, EP1K10TC100-3 Datasheet - Page 19

EP1K10TC100-3
Manufacturer Part Number
EP1K10TC100-3
Description
IC ACEX 1K FPGA 10K 100-TQFP
Manufacturer
Altera
Series
ACEX-1K®r
Datasheet
1.EP1K10TC100-3N.pdf
(86 pages)
Specifications of EP1K10TC100-3
Number Of Logic Elements/cells
576
Number Of Labs/clbs
72
Total Ram Bits
12288
Number Of I /o
66
Number Of Gates
56000
Voltage - Supply
2.375 V ~ 2.625 V
Mounting Type
Surface Mount
Operating Temperature
0°C ~ 70°C
Package / Case
100-TQFP, 100-VQFP
Lead Free Status / RoHS Status
Contains lead / RoHS non-compliant
Other names
544-1027
Available stocks
Company
Part Number
Manufacturer
Quantity
Price
Part Number:
EP1K10TC100-3
Manufacturer:
ALTERA/阿尔特拉
Quantity:
20 000
Part Number:
EP1K10TC100-3N
Manufacturer:
ALTERA/阿尔特拉
Quantity:
20 000
Altera Corporation
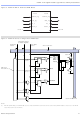
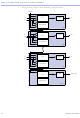
Figure 10. ACEX 1K Cascade Chain Operation
d[(4 n – 1)..(4 n – 4)]
AND Cascade Chain
d[3..0]
d[7..4]
Cascade Chain
With the cascade chain, the ACEX 1K architecture can implement
functions that have a very wide fan-in. Adjacent LUTs can be used to
compute portions of the function in parallel; the cascade chain serially
connects the intermediate values. The cascade chain can use a logical AND
or logical OR (via De Morgan’s inversion) to connect the outputs of
adjacent LEs. With a delay as low as 0.6 ns per LE, each additional LE
provides four more inputs to the effective width of a function. Cascade
chain logic can be created automatically by the compiler during design
processing, or manually by the designer during design entry.
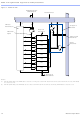
Cascade chains longer than eight bits are implemented automatically by
linking several LABs together. For easier routing, a long cascade chain
skips every other LAB in a row. A cascade chain longer than one LAB
skips either from even-numbered LAB to even-numbered LAB, or from
odd-numbered LAB to odd-numbered LAB (e.g., the last LE of the first
LAB in a row cascades to the first LE of the third LAB). The cascade chain
does not cross the center of the row (e.g., in the EP1K50 device, the cascade
chain stops at the eighteenth LAB, and a new one begins at the nineteenth
LAB). This break is due to the EAB’s placement in the middle of the row.
Figure 10
form functions with a wide fan-in. These examples show functions of 4n
variables implemented with n LEs. The LE delay is 1.3 ns; the cascade
chain delay is 0.6 ns. With the cascade chain, decoding a 16-bit address
requires 3.1 ns.
LUT
LUT
LUT
shows how the cascade function can connect adjacent LEs to
LE n
LE1
LE2
ACEX 1K Programmable Logic Device Family Data Sheet
d[(4 n – 1)..(4 n – 4)]
OR Cascade Chain
d[3..0]
d[7..4]
LUT
LUT
LUT
LE n
LE1
LE2
19
13